

퍼셉트론 (Perceptron)
저번 포스팅에 이어 학습!!
2022.11.26 - [분류 전체보기] - 딥러닝 기초 - 퍼셉트론(Perceptron) (1)
2. 단층 퍼셉트론 (Single-Layer Perceptron)
perceptron learning
퍼셉트론은 단층 퍼셉트론과 다층 퍼셉트론으로 나뉘어진다. 단층 퍼셉트론은 입력층과 출력층 단 두 단계로만 이루어진다.
퍼셉트론의 수학 식이 다음과 같았다.
$$
\hat{y} = \begin{cases} +1 & if\ \sum_i^{n}w_ix_i + b \geq 0 \\ -1\ or\ 0 & otherwise\end{cases}
$$
x는 입력값이므로 이 수학 식에서 우리가 찾아야 하는 파라미터는 weight($w$)와 bias(b) 라고 할 수 있다. 이 두 값의 따라 모델의 출력이 달라지기 때문이다.
$\hat{y}$만 봤을 때 다음 식으로 볼 수 있는데,
$$
\hat{y} = w_0 + w_1x_1 + ... + w_nx_n
$$
이 식은 다음과 같이 표현될 수 있다.
$$
w_i \leftarrow w_i + \Delta w_i
$$
유도과정
위의 식을 도출하기 위해선 아래의 식에서 출발한다.
$$
E[w] \equiv \frac{1}{2}\sum_{d \in D} (y_d - \hat{y}_d)^2
$$
- $y_d$ : target
- $\hat{y}_d$ : output
- $\hat{y} = w_0 + w_1x_1 + ... + w_nx_n$
주어진 입력 x에 대한 신경망이 계산한 (추측한) $\hat{y}$과 정답 y의 차이에 관한 식이다.
$y_d$의 의미?
- 실제값, target 값, 목표값
$\hat{y}$의 의미?
- 예측값
$y_d - \hat{y}_d$ = 정답과 신경망이 계산한 (추측한) 값의 차이
- Cost가 최소가 되는 W를 찾는 것이 목표 !!
$(y_d - \hat{y}_d)^2$ 이 식을 보아 이차방정식 임을 알 수 있는데, 우리의 목표는 정답 y와 신경망이 계산한 \hat{y}의 차이가 가장 최소가 되는 지점. 즉, 이차방정식의 최소가 되는 지점의 w값을 구하는 것이다.
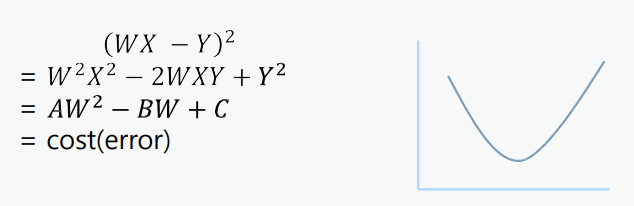
- $WX$ = 모델이 예측한 값 :point_right: x값 : w(weight), y값 : E (cost)
이차 방정식을 풀면 위의 풀이가 나오는데, 이 식에서 양변을 미분한다면
$$
W = W - \frac{\partial}{\partial W} cost(W) = W - \Delta W
$$
이런 식이 나오게 된다. 다음 W = 현재 W - 현재 W의 cost를 미분을 뜻한다.
우리가 원하는 weight $w$를 찾는 방법
Cost가 최소가 되는 $w$를 찾는다.
$w$의 값을 구하는 방법은
- 1. 각각의 가중치에 대해 임의의 값을 설정한다.
- 2. 잘 될 때까지 값을 조금씩 변경한다.
로 줄일 수 있다.
$w$를 찾는 방법 중 임의의 값을 설정했다면 다음은 최적의 값을 찾아야 한다.
다음 그림을 참고해서 이해하면 편하다.
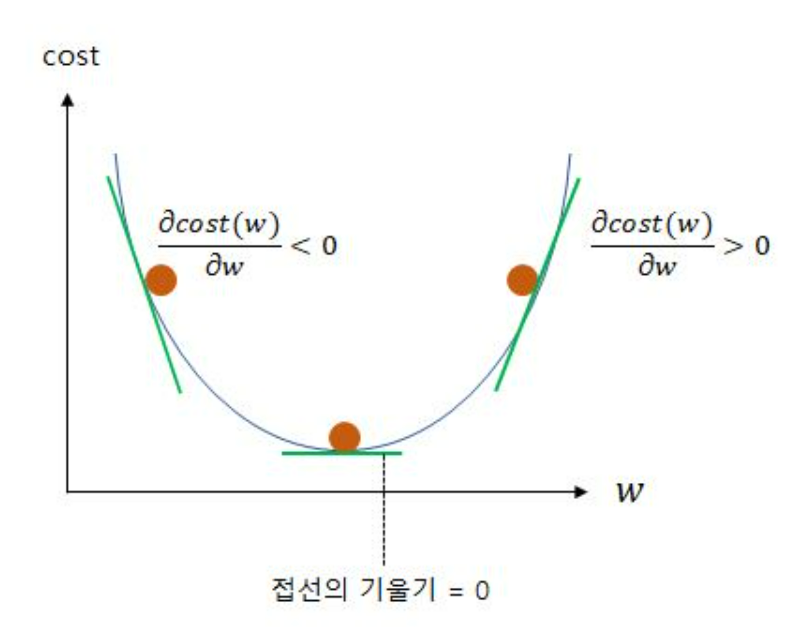
- 처음 설정한 W값이 최소 값의 오른쪽이었다면 기존의 값에서 조금 빼준다.
$$
\Delta w_i = 음수 for\ w^2
$$+방향 기울기인 상태에서 반대 방향으로 가는 것이 목표이기 때문에 기울기에-를 붙인다. - 처음 설정한 W값이 최소 값의 왼쪽이었다면 기존의 값에서 조금 더해준다.
$$
\Delta w_i = 양수 for\ w^b
$$
마찬가지로-방향 기울기 상태에서 반대 방향으로 가는 것이 목표이기 때문에 기울기에+를 붙인다.
이때 중요한 것은 아주 조금씩 갱신되도록 하는 것이다. 갱신 값이 크면 최소값 주위에서 최소값을 찾지 못하고 진동할 수도 있다.
그리고 $\Delta w_i$를 다음으로 정의할 수 있는데,
$$
\Delta w_0 = - \eta \frac{\partial E}{\partial w_0} = \eta \sum_d (y_d - \hat{y}_d)
$$
$\eta$는 학습률 (learning rate)라 부른다. 학습률을 적당히 0.001, 0.0001... 작은 값을 곱해주며 갱신해 준다.
이 방법을 경사하강법 (Gradient Descent Method) 라 부른다.
경사하강법은 다음에 더 공부하기로 하자.
유도과정
- 편미분이용
(1)
$ \frac{\partial}{\partial w_i} = \frac{\partial}{\partial w_i} \frac{1}{2} \sum_d (y_d - \hat{y_d})^2 $
$ = \frac{1}{2} \sum_d {\frac{\partial}{\partial w_i} (y_d - \hat{y_d})^2}$
$ = \frac{1}{2} \sum_d 2 (y_d - \hat{y_d}){\frac{\partial}{\partial w_i} (y_d - \hat{y_d})}$
$ = \sum_d (y_d - \hat{y_d}) {\frac{\partial}{\partial w_i} (y_d - w_0 -w_1x_{d,1}-w_ix_{d,i}-...-w_nx_{d,n})}$
$ = \sum_d (y_d - \hat{y_d}) (-x_{d,i})$
(2) 정리
$\frac{\partial}{\partial w_i} = \sum_d (y_d - \hat{y_d}) (-x_{d,i})$
$\frac{\partial}{\partial w_0} = \sum_d (y_d - \hat{y}_d) (-1)$
(3) 최종 결과
$weight = \Delta w_i = -\eta\frac{\partial E}{\partial w_i} = \eta \sum_d (y_d - \hat{y_d}) (x_{d,i})$
$bias = \Delta w_0 = -\eta\frac{\partial E}{\partial w_0} = \eta \sum_d (y_d - \hat{y_d})$