모두의 인공지능 기초 수학 Chapter 14 복습
# 베이지안 확률
B일 때 A일 확률
$$P(A|B) = \frac{A(B|A)P(A) }{P(B)} $$
$$P(B) = P(B \cap A) +P(B \cap A')$$
$$P(A|B) = \frac{P(B|A)P(A)}{P(B|A)P(A)+P(B|A')P(A')} $$
# 베이지안 이론
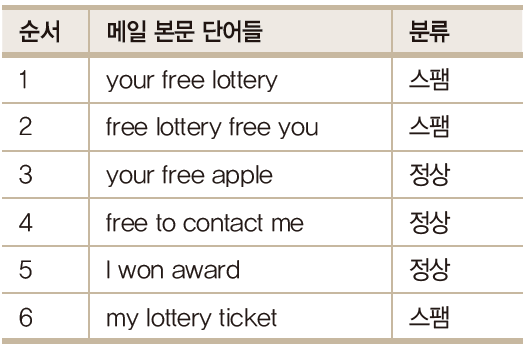
- 스팸메일 필터
- 메일본문(입력 테스트)을 이용하여 메일이 스팸인지 구분하는 예시를 살펴보자
- 메일의 스팸 유무
$$P(정상메일 | 메일본문) = 메일본문이 정상일 확률$$
$$P(스팸메일 | 메일본문) = 메일본문이 스팸일 확률$$
* 나이브베이즈
베이즈 모델 :
$$P(A|B) = \frac{P(B|A)P(A)}{P(B)} $$
이 조건부 확률을 이용 (B가 있을 때 A일 확률)
A를 문서 카테고리, B를 문서라고 가정했을 때, 해당 문서가 있을 때, 해당 카테고리일 확률
P(A1|B)와 P(A2|B)를 비교해서 확률이 더 높은 값을 분류하기 위함
이런 비교 계산을 하기 위해 공통되는 P(B) 제거하면
$$P(A|B) = P(B|A)P(A)$$
A 카테고리일 때, W1, W2, ..., Wn 단어가 있다고 가정하면
$$P(A|B) = P(W1,W2,...,Wn|C)P(C)$$
>> Naive Bayes : 각각의 단어가 A 카테고리에 독립적이라는 나이브한 가정을 둠으로써 계산
$$P(C|D) = P(W1|C)P(W2|C)...P(Wn|c)P(C) = \prod P(W|C)P(C) $$
- 나이브 베이즈를 이용하여 정리하면
$$P(정상메일 | 메일본문) = \frac{ P(메일본문 | 정상메일) X P(정상메일)}{P(메일본문)}$$
$$P(스팸메일 | 메일본문) = \frac{ P(스팸본문 | 정상메일) X P(정상메일)}{P(스팸본문)}$$
입력 텍스트가 주어졌을 때, P(정상메일|메일본문)이 P(스팸메일|메일본문)보다 크면 정상, 그렇지 않으면 스팸
본문에 단어가 두 개 있다고 가정했을 때 단어를 W1, W2라고 하고,
이 식을 간단히 하면
$$P(정상메일 | 메일본문) = P(W1 | 정상메일) X P(W2 | 정상메일) X P(정상메일)$$
$$P(스팸메일 | 메일본문) = P(W1 | 스팸메일) X P(W2 | 스팸메일) X P(스팸메일)$$

- 입력 테스트 "my free lottery" 있다고 하면
$$P(정상메일 | 메일본문) = P(my | 정상메일) X P(free | 정상메일) X P(lottery | 정상메일) X P(정상메일)$$
$$P(스팸메일 | 메일본문) = P(my | 스팸메일) X P(free | 스팸메일) X P(lottery | 스팸메일) X P(스팸메일)$$
- P(정상메일) = P(스팸메일) = 총 메일여섯 개 중 세 개 = 0.5
>> 두 식 확률 같으므로 생략 가능
$$P(정상메일 | 메일본문) = P(my | 정상메일) X P(free | 정상메일) X P(lottery | 정상메일) $$
$$P(스팸메일 | 메일본문) = P(my | 스팸메일) X P(free | 스팸메일) X P(lottery | 스팸메일) $$
- P(my | 정상메일)을 구하는 방법
$$\frac{정상메일에서 my가 등장한 총 빈도수}{정상메일에 등장한 모든 단어의 빈도수 총합}$$
- 이런 원리로 "my free lottery"를 분류해보면
$$P(정상메일 | 메일본문) = \frac{0}{10} \times \frac{2}{10} \times \frac{0}{10} = 0$$
$$P(스팸메일 | 메일본문) = \frac{1}{10} \times \frac{3}{10} \times \frac{3}{10} = 0.009$$
>> "my free lottery" 는 스팸메일
# 라이브러리 호출
import numpy as np
import pandas as pd
from nltk.corpus import stopwords
import string
import nltk
# corpus : 말뭉치
# stopwords : 불용어
df = pd.read_csv('spam.csv')
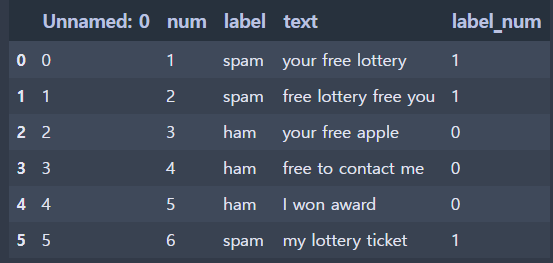
>> 라이브러리 호출하고 csv 파일을 불러온다
>> from nltk.corpus import stopwords :
데이터에서 유의미한 단어 토큰만 선별하기 위해서는 큰 의미가 없는 토큰을 제거하는 작업이 필요.
' I, my, me, over, 조사, 접미사' 같은 단어들은 실제 의미 분석하는데 거의 기여X
>> 이런 단어들을 불용어(stopword)
def process_text(text):
# text에서 구두점(punctuation) 삭제
nopunc = [char for char in text if char not in string.punctuation]
nopunc = ''.join(nopunc)
# text에서 불용어(접미사, 조사 등) 삭제
cleaned_words = [word for word in nopunc.split()
if word.lower() not in stopwords.words('english')]
return cleaned_words>> process_text를 정의하여 데이터 프레임 'df'에 있는 'text'를 토큰화 시키고자 함
>> 1. text에서 구두점(punctuation) 삭제
string.punctuaion : 영어로 구두점으로 간주되는 모든 문자를 포함
이 목록을 제외함으로써 문자열에서 모든 구두점을 제외 할 수 있음
text에서 string.punctuation이 아닌 char만 char에 넣고 nopunc라고 해줘
join() 함수를 이용해서 nopunc를 정제해서 nopuc에 저장해줘
>> 2. text에서 불용어 삭제
stopwords.words('english') : 영어사전에서 제공하는 영어의 불용어 리스트
이 리스트를 제외하고 소문자로 만들어 리스트에 넣음
punctuation이 없는 정제된 nopunc에서 word를 불러오는데 불용어(stopwords)가 없는 것만 뽑아서 word에 넣어줘 대신
lower(소문자)로 만들어서 리스트에 저장해줘.
process_text에 text에 넣고 반환
df['text'].apply(process_text)
>> 정의한 process_text의 text 결과
punctuation과 불용어가 삭제됨
# text를 토큰화한 뒤, 토큰 수의 행렬 변환
from sklearn.feature_extraction.text import CountVectorizer
messages_bow = CountVectorizer(analyzer = process_text).fit_transform(df['text'])
>> Scikit-Learn의 서브 패키지 feature_extraction에서 CountVectorizer 클래스 호출
문서 집합에서 단어 토큰을 생성하고 각 단어의 수를 세어 BOW 인코딩 벡터를 만드는 클래스
(BOW 인코딩 : 문서를 숫자 벡터로 변환하는 방법)
1. 문서를 토큰 리스트로 변환
2. 각 문서에서 토큰의 출현 빈도를 셈
3. 각 문서를 BOW 인코딩 벡터로 변환
analyzer 인수로 사용할 토큰 생성기를 'process_text'로 함
fit_transform() 은 fit()과 transform()을 한번에 처리할 수 있게 하는 메서드
fit()은 데이터를 학습시키는 메서드이고, transform()은 실제로 학습시킨 것을 적용하는 메서드
CountVectorizer 클래스를 이용해 process_text로 단어 토큰을 생성하고 각 단어의 수를 셈
이때, 학습시키고 적용할 문서는 df['text']
단어의 수를 행렬로 변환시켜서 messages_bow라고 함
# train data, test data 8:2 비율로 구분
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(messages_bow, df['label_num'], test_size = 0.2, random_state = 42)
# test_size는 0.2 train size는 자동적으로 0.8
# 랜덤하게 섞은것 중에 여러 세트가 있는데 42번으로 했을 떄 제일 잘 나옴
# 랜덤하게 섞은 데이터로 다른 알고리즘으로 적용해보고 싶을 때 random_state를 꼭 해줘야함>> Scikit-Learn의 서브 패키지 model_selection에서 train_test_split 클래스 호출
>> train / test를 분리하는 이유는 머신러닝 모델에 train 데이터를 100% 학습시킨 후 test데이터에 모델을 적용했을 떄 성능이 생각보다 않나오는 경우가 많음 >> overfitting
모델이 내가 가진 학습 데이터에 너무 과적합되도록 학습한 나머지, 이를 조금이라도 벗어난 케이스는 예측률이 현저히 떨어지기 때문
>> overfitting을 방지하기 위해 validation set으로 모델 평가
>> test_size를 0.2, train_size를 0.8로 지정
random_state : 세트를 섞을 때 해당 int 값을 보고 섞는데, 이 값을 고정해야 매번 데이터 셋이 변경되지 않음
>> x_train : train data set의 feature
x_test : test data set의 feature
y_train : train data set의 label
y_test : test data set의 label
messages_bow를 feature 부분으로, df['label_num']을 label 부분으로 하여 test와 train 비율을 2:8로 하여 모델 학습
(label_num = spam mail 이면 1, 정상메일이면 0)
# 나이브 베이즈 모델 적용, 훈련
# 훈련(train)>> 모델 생성
from sklearn.naive_bayes import MultinomialNB
classifier = MultinomialNB()
classifier.fit(X_train, y_train) # 훈련시, 반드시 train data 사용>> Scikit-Learn의 서브 패키지 naive_bayes에서 MultinomialNB 클래스 호출
>> MultinomialNB 모델을 classifier에 저장하고 X_train, y_train 데이터를 학습
# 훈련용 데이터로 예측해서 비교해 봄
classifier.predict(X_train) # 예측값
y_train.values # 실제값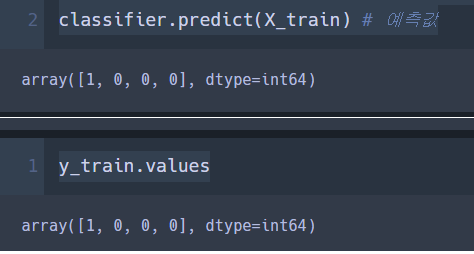
>> predict를 사용하면 0과 1만 반환하는데 0은 정상메일 1은 스팸메일이다.
- 학습 데이터셋에서 모델의 정확도를 표현해보자
# 학습 데이터셋에서 모델의 정확도 표현하기
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix, accuracy_score
pred = classifier.predict(X_train)
# metrics pkg >> prescision(정밀도), recall(재현율), f1 score(f1 스코어) 점수 구하기
print(classification_report(y_train, pred))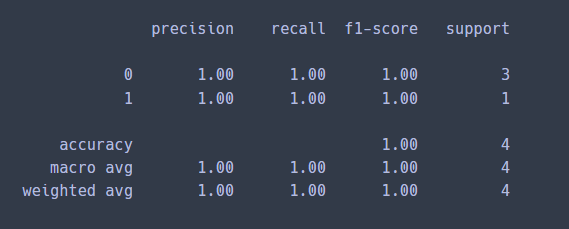
>> Scikit-Learn의 matrics 패키지에서 classification_report를 보면
y_train(실제값)과 classifier.predict(X_train) (예측값)을 비교했을 때 정밀도, 재현율, f1 스코어 모두 1로 높은 값으로 나왔다.
# 혼동행렬(confusion matrix)
print('confusion Matrix: \n', confusion_matrix(y_train, pred))
print()
print('Accuracy: ', accuracy_score(y_train, pred))
>> 혼동행렬
실제\예측 N P
N TN FN
P FN TP
* 정상메일 = 0, 스팸메일 = 1
TN = True Negative, 정상메일을 정상메일으로 예측 (정답) 3
FP = False Positive, 정상메일이 아닌 것을 정상메일이라고 예측 0
FN = False Negative, 정상메일을 정상메일이 아니라고 예측 0
TP = True Positive, 정상메일이 아닌 것을 정상메일이 아니라고 예측(정답) 1
>> 1) precision = 정밀도
Positive 라고 예측한 샘플(TP + FP) 중 실제로 Positive인 샘플(TP) 비율
'예측값' 기준 '정답인 예측값'
$$precision = \frac{TP}{TP+FP}$$
>> 2) Recall = 재현율
실제 Positive인 샘플(TP+FN) 중 Positive라고 예측한 샘플(TP) 비율
'실제값' 기준 '정답인 예측값'
$$Recall = \frac{TP}{TP+FN}$$
>> 3) Accuracy = 정확도
전체 샘플 중 맞게 예측한 샘플의 비율
$$Accuracy = \frac{TP+TN}{TN+TP+FN+FP}$$
>> 4) F1-score
F-score 란 precision과 recall의 가중 조화평균
$$F_\beta = \frac{(1+ \beta ^2)(precision \times recall)}{\beta^2 precision + recall}$$
이때 가중치를 1인 경우를 F1-score
$$ F_1 = \frac{(1+ 1^2)(precision \times recall)}{1^2 precision + recall}$$
>>
$$ F_1 = \frac{(2)(precision \times recall)}{precision + recall}$$
>> 5) support = 각 라벨의 실제 샘플 개수
4개의 샘플 중 라벨이 0 (정상메일)인 샘플은 3개
+ 민감도(Sensitivity)
$$Sensitivity = \frac{True Positive}{True Positives + False Negatives}$$
+ 특이도 (Specificity)
$$Specificity = \frac{True Negatives}{True Negatives + False Positives}$$
>> 6) macro avg : 단순 평균
>> 7) weight avg : 가중 평균
- test data에 적용
# test data에 적용 (모델의 성능)
classifier.predict(X_test) # 예측값
print('Actual value: ',y_test.values) # 실제값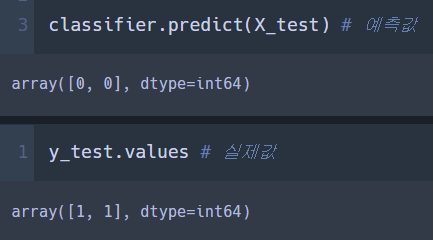
>> train 데이터와 달라짐
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix, accuracy_score
pred = classifier.predict(X_test)
print(classification_report(y_test, pred))
print(confusion_matrix(y_test,pred))
accuracy_score(y_test, pred)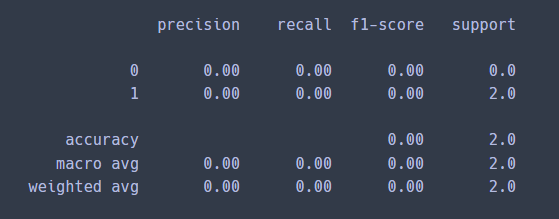
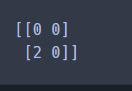
>> 실제 test 데이터에 적용했을 때는 precision, recall, f1-score 모두 0으로 나옴