[퀀트] 자본자산가격결정모델(CAPM) (2) [python]

파이썬으로 배우는 포트폴리오 study day8
지난 포스팅에 이어 CAPM을 알아보자.
2022.12.04 - [TIL/09_QUANT] - [퀀트] 자본자산가격결정모델(CAPM) (1) [python]
[퀀트] 자본자산가격결정모델(CAPM) (1) [python]
파이썬으로 배우는 포트폴리오 study day7 오늘은 내가 퀀트를 공부하게 된 계기랄까.. [메타코드] 유튜브 채널에서 처음 접하게 된 CAPM을 이 책을 통해 다시 공부하게 되었다. 이미 한 번 접한 내용
joo-code.tistory.com
오늘은 CAPM의 증권시장선과 자본시장선, 최소분산포트폴리오 진행
자본자산가격결정모델
증권시장선과 자본시장선
앞의 포스팅에서 살펴봤었던 증권시장선(SML)과 이펀 포스팅에서 공부할 자본시장선(CML)을 비교해보자.
- 증권시장선(SML) : 시장에서 거래되는 모든 자산에 대해 균형 상태에서 위험과 수익률 간 관계 설명
- 자본시장선(CML) : 효율적 포트폴리오에 증권시장선을 적용한 경우
자본시장선(CML)
$$
E(R_p) = R_f + \frac{E(R_m) - R_f}{\sigma_m}\sigma_p
$$
자본시장선의 기대수익률은 무위험이자율 + 위험프리미엄인데, 위험프리미엄은 위험의 균형 가격 x 위험 수량을 의미한다.
자본시장선의 기울기 $\frac{E(R_m)-R_f}{\sigma_m}$ 는 시장에서 위험 한 단위에 대한 위험보상이며 위험에 대한 균형가격을 의미한다. 즉, 샤프비율을 말한다.
샤프지수
투자 기간 동안 발생한 수익률을 위험(변동성)과 비교하여, 위험 대비 보상을 비교하는 지표
자본시장선의 "기울기" ->
- 자산을 비교하기 위한 수단
자본시장선 포트폴리오는 체계적 위험으로 이뤄지며, 효율적 포트폴리오다. 따라서 비효율적 포트폴리오의 기대수익률과 위험 간의 관계는 설명하지 못한다.
증권시장선(SML)
증권시장선은 균형자본시장에서 개별 증권 i의 체계적 위험 척도인 베타와 기대수익률의 가격 결정 관계를 설명해준다.
증권시장선의 기대수익률 역시 무위험이자율 + 위험프리미엄인데, 위험프리미엄은 시장위험 프리미엄 x 베타계수
$$
E(R_i) = R_f + (E(R_m) - R_f) \beta_i
$$

증권시장선의 특징
- 증권의 기대수익률은 베타가 결정한다. (나머지(비체계적 위험)는 영향을 주지 않는다.)
- 두 증권의 베타 위험이 같다면 기대수익률도 같다.
- 증권의 기대수익률과 베타는 선형관계
- 자산 i의 위험프리미엄은 공분산위험(\sigma_{im})에 비례
- SML 기울기(시장위험프리미엄 $E(R_m)-R_f$은 양의 값을 가진다.
- E(R_m) - R_f > 0
- 따라서 시장위험이 크고, 투자자의 위험회피 정도가 클수록 시장 위험프리미엄이 커지므로 SML 기울기도 커진다.
- SML 절편은 명목 무위험이자율을 나타내므로 그 크기는 실질 무위험이자율과 예상 인플레이션율에 의해 결정
- 명목이자율 : 거시경제변수의 변화에 따라 상하로 이동
시장베타는 1 ($\beta_m = 1$)
- $\beta_i > 1$ : 시장위험프리미엄보다 큰 초과수익률 획득 = 공격적 주식
- $\beta_i < 1$ : 시장프리미엄보다 적은 초과수익률 획득 = 방어적 주식
이러한 증권시장선과 자본시장선을 수학적으로 살펴보자.
증권시장선(SML)의 식은 다음과 같았다.
$$
E(R_p) = R_f + \frac{E(R_m) - R_f}{\sigma_m}\sigma_p
$$
이를 변형시켜보면,
$$
E(r_i) - r_f = [E(r_m)-r_f] \beta_i
$$
$$
\frac{E(r_i)-r_f}{\beta_i}} = E(r_m)-r_f
$$
가 성립한다.
즉, 마지막 등식을 보면 우변은 개별주식 i에 관계없이 결정되므로, 이 식은 베타 한 단위에 대한 위험보상이 모든 위험자산에 대해 일정하며 시장포트폴리오의 위험프리미엄과 같게 됨을 의미한다.
한편, CAPM의 효율적 포트폴리오 P의 체계적 위험 $\beta$는 다음과 같은 정의를 가지고 있다.
베타
분산 불가능한 위험, 시장위험 또는 체계적 위험
$$
\beta_P = \frac{\sigma_{Pm}}{\sigma_m^2} = \frac{\rho_{Pm} \sigma_P}{\sigma_m} = \frac{Cov(r_P,r_m)}{Var(r_m)}
$$
이 베타를 증권시장선에 대입해보면,
$$
E(r_P) = r_f + [\frac{E(r_m)-r_f}{\sigma_m}]\frac{\sigma_{Pm}}{\sigma_m}
$$
$\sigma_{Pm} = \rho_{Pm}\sigma_P\sigma_m$ 이므로 이를 대입하면
$$
E(r_P) = r_f + [\frac{E(r_m)-r_f}{\sigma_m}] \rho_{Pm}\sigma_P
$$
그리고, 자본시장선 상에 있는 효율적 포트폴리오들의 경우 $\rho_{Pm}=1$이다.
따라서
$$
E(r_P) = r_f + [\frac{E(r_m)-r_f}{\sigma_m}] \sigma_P
$$
와 같은데 이는 CML 식과 동일하다.
즉, SML은 균형상태에서 CML을 포괄하는 식이고, 시장의 모든 자산에 대해 균형가격결정 원칙을 제공한다.
과대평가주식과 과소평가주식의 식별 방법
증권시장선을 이용하여 주식의 가치평가를 할 수 있다.
개별증권 i의 베타($\beta_i$)에 대응한 균형기대수익률 E(r_i)는 SML 상에 위치한다. 이 때의 주식가격은 적정가격으로서 기업의 내재가치를 반영한다.
- 저평가(과소평가) 주식 : SML 위쪽에 위치
- 고평가(과대평가) 주식 : SML 아래쪽에 위치
투자자는 과소/과대평가된 주식들의 매매를 통해 이익 가능하다.
- 과소평가 주식 : 매입 증가 -> 주가 상승 -> 기대수익률 하락 -> SML 상에 위치하여 균형에 도달
- 과대평가 주식 : 매도 증가 -> 주가 하락 -> 기대수익률 상승 -> SML 상에 위치하여 균형에 도달

과소평가 : 주식 A, B, C
과대평가 : 주식 X, Y, Z
포트폴리오 최적화
포트폴리오 최적화는 샤프비율과 같은 평균-분산 효용함수를 극대화하는 투자자산의 비중을 구하는 것이다.
샤프비율이 가장 높은 최적 포트폴리오는 자본시장선과 효율적 포트폴리오 접선 위에 위치한다.
파이썬 패키지 scipy를 이용하여 포트폴리오 최적화를 할 수 있다.
https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html
scipy.optimize.minimize(
fun, # 목적함수
x0, # 초깃값
args=(), # 초깃값 외에 목적함수에 전달할 매개변수
method=None, # 최적화 해 찾기 종류
jac=None, hess=None, hessp=None,
bounds=None, # 경계값
constraints=(), # 제약조건
tol=None, callback=None, options=None)
예제 1
- 목적함수(최솟값) y = x + 1
- 목적함수는 우리가 풀고자 하는 식이나 모델
- 초깃값 : = -1.0
- 초깃값은 해가 존재할 만한 값을 정하는 것이 좋다.
- 제약조건 x >= 3
- x값의 범위를 정하는 것 (-1 <= x <= 6)
- 최적화 메서드 : 포트폴리오 최적화를 위해 사용할 메서드는 SLSQP 메서드
최적화 알고리즘 SLSQP
최적화 : 특정 집합 위에서 정의된 실숫값, 함수, 정수에 대해 그 값이 최대나 최소가 되는 상태
SLSQP : 복잡한 현실 문제를 단순화해 목적함수를 이차식으로 근사해 풀고 다음 번 지점을 예측해 다시 동일한 방법을 수행하는 문제를 푸는 알고리즘
# 1. 패키지 불러오기
from scipy.optimize import minimize
# 2. 목적함수
def obj1(x):
return x+1
# 3. 제약식
def const(x):
return x-3
# 제약조건을 적을 때는 식을 한쪽으로 다 치환하여 한 변을 0으로 만들어주어야 한다.
# 4. 초깃값. -> 리스트 형태
x0 = [-1]
# 5. 해의 범위 -> 튜플() 형태
b = (-1, 6)
# 6. 범위 튜플
# 만일 여러 변수의 범위를 설정한다면 여러 개의 범위 투플을 넣음
bnd = (b, )
# 7. 제약조건 -> 딕셔너리 {}
con = {'type':'ineq', 'fun':const}
# type : 'eq' or 'ineq' (0과 같거나 or 같지 않거나)
# fun : 제약식 함수 (문자열 아님 주의!)
# 8. 최적화 함수
sol = minimize(obj1, x0, method='SLSQP', bounds=bnd, constraints=con)
print(sol)
print(sol.x)
결과
fun: 3.9999999999999885
jac: array([1.])
message: 'Optimization terminated successfully'
nfev: 4
nit: 2
njev: 2
status: 0
success: True
x: array([3.]) >> y 값을 최소화하는 x 값
예제 2
- 목적함수 $minx1x4(x1 + x2 + x3) + x3$
- 제약조건
- $x1x2x3x4 ≥ 25$
- $x1^2 + x2^2 + x3^2 + x4^2 = 40$
- 범위 $ 1 ≤ x1,x2,x3,x4 ≤ 5$
- 초깃값 x1 = 1, x2 = 5, x3 = 5, x4 = 1
# 라이브러리
from scipy.optimize import minimize
import numpy as np
# 1. 목적함수 정의
def obj2(x):
x1 = x[0]
x2 = x[1]
x3 = x[2]
x4 = x[3]
return x1*x4*(x1+x2+x3) + x3
# 2. 제약조건
def const1(x):
return x[0] * x[1] * x[2] * x[3] - 25
def const2(x):
sum_sq = np.sum(np.square(x))
return sum_sq - 40
# 3. 초깃값
x0 = [1, 5, 5, 1]
# 4. 해의 범위
b = (1, 5)
# 5. 범위 튜플
bnds = (b, b, b, b)
# 6. 제약 조건
# const1 : >= 이므로 ineq, const2 : = 이므로 eq
con1 = {'type':'ineq', 'fun':const1}
con2 = {'type':'eq', 'fun':const2}
cons = [con1, con2]
# 7. 최적화 함수
sol = minimize(obj2, x0, method='SLSQP', bounds=bnds, constraints=cons)
print(sol)
결과
fun: 17.01401724556073
jac: array([14.57227039, 1.37940764, 2.37940764, 9.56415081])
message: 'Optimization terminated successfully'
nfev: 25
nit: 5
njev: 5
status: 0
success: True
x: array([1. , 4.74299607, 3.82115466, 1.37940764])
포트폴리오 최적화 python code
이번에는 밑의 포스팅에서 진행했던 효율적 투자선의 코드를 이용해 최소분산포트폴리오를 찾아보자.
2022.12.02 - [TIL/09_QUANT] - [퀀트] 평균-분산 포트폴리오 이론 (3) [python]
위의 코드에 이어서 진행!!
(샤프지수 이용부분은 일부 겹침..)
SLSQP 이용 최소분산포트폴리오
# 라이브러리
from scipy.optimize import minimize
# 위험 최소화. 포트폴리오 분산 함수를 목적함수
def obj_variance( weights, covmat ):
return np.sqrt( weights.T @ covmat @ weights )
# 목적함수 obj_variance()에 사용되는 공분산 행렬
# 일간수익률 공분산을 연간으로 환산
covmat = cov_daily * 252
# 투자 자금을 다섯 종목에 균등하게 20%씩 투자
weights = np.array( [ 0.2, 0.2, 0.2, 0.2, 0.2 ] )
# 각 종목의 투자 비중 한도 0~100%이며 튜플로 지정
bnds = ( (0,1), (0,1), (0,1), (0,1), (0,1) )
# 제약조건은 투자 비중 100%(무차입투자)
cons = ({ 'type': 'eq', 'fun': lambda x: np.sum(x) - 1 })
# ∑x = 1.0 -> ∑x - 1 = 0
# 최적화
res = minimize( obj_variance, weights, (covmat), method='SLSQP', bounds=bnds, constraints=cons )
# 결과 출력(마지막 x 값이 최적화된 투자 비중)
print(res) fun: 0.186660635185886
jac: array([0.18674867, 0.18674396, 0.18687719, 0.18621498, 0.22987829])
message: 'Optimization terminated successfully'
nfev: 48
nit: 8
njev: 8
status: 0
success: True
x: array([2.60359547e-01, 5.18690026e-02, 4.21719382e-01, 2.66052068e-01,
7.48099499e-18])
# 일간수익률 평균과 최적화로 얻은 투자 비중을 곱해 최소분산포트폴리오이 기대수익률 구하기
rets = np.sum(ret_daily.mean() * res['x']) * 252
# 최소분산포트폴리오의 위험
vol = np.sqrt(res['x'].T @covmat @res['x'])
colors = np.random.randint(0, n_ports, n_ports)
plt.style.use('Solarize_Light2')
# 분산 차트 설정
plt.scatter(p_volatility, p_returns, c='grey', marker='o', cmap=mpl.cm.jet)
plt.scatter(vol, rets, marker='*', s=500, alpha=1.0, c='red')
# x축 라벨
plt.xlabel('Volatility(Std. Devation)')
# y축 라벨
plt.ylabel('Expected Returns')
# 차트 제목
plt.title('Efficient Frontier')
plt.show()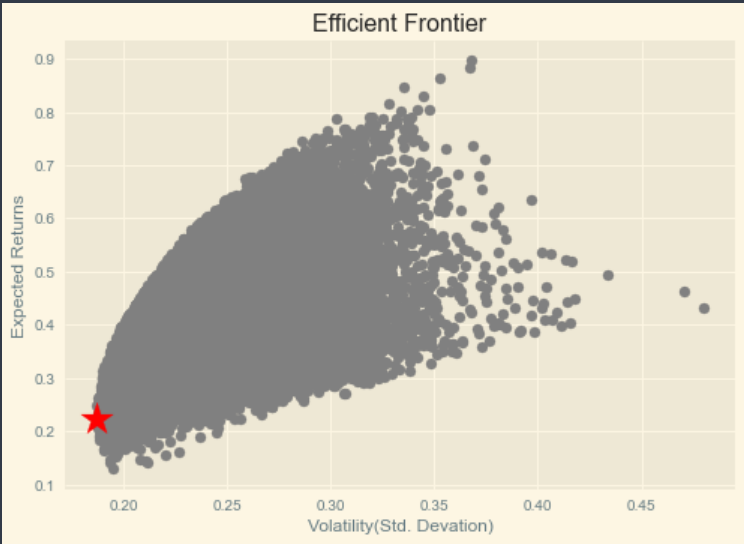
샤프비율 최적화를 이용한 최소분산포트폴리오 투자 비중
샤프비율은 위험 한 단위당 얻을 수 있는 수익의 크기이다.
따라서 샤프비율은 포트폴리오 위험을 최대화해야 최적화를 할 수 있다.
목적함수 :
$$
\frac{1}{sharpe\ ratio}
$$
# 라이브러리
from scipy.optimize import minimize
# 목적함수
def obj_sharpe(weights, returns, covmat, rf):
ret = np.dot(weights, returns)
vol = np.sqrt(np.dot(weights.T, np.dot(covmat, weights)))
return 1 / ((ret-rf) / np.sqrt(vol))
# 종목 개수와 공분산
n_assets = len(tickers)
covmat = cov_daily * 252
# 무위험수익률
rf = 0.01
# 초기 투자 비중 = 종목 개수만큼 균등함
weights = np.ones([n_assets]) / n_assets
# 투자 비중의 범위 0~100%
bnds = tuple((0., 1.) for i in range(n_assets))
# 제약 조건 함수
def const1(x):
return x[0] * x[1] * x[2] * x[3] - 25
def const2(x):
sum_sq = np.sum(np.square(x))
return sum_sq - 40
cons = ({'type':'eq', 'fun': lambda w: np.sum(w) - 1})
# 최적화 함수
res = minimize(obj_sharpe, weights, (ret_annual, covmat, rf),
method='SLSQP', bounds=bnds, constraints=cons)
p_returns = [ ]
p_volatility = [ ]
p_weights = [ ]
n_assets = len( tickers )
n_ports = 30000
for s in range( n_ports ):
wgt = np.random.random( n_assets )
wgt /= np.sum( wgt )
ret = np.dot( wgt, ret_annual )
vol = np.sqrt( np.dot( wgt.T, np.dot(cov_annual, wgt ) ) )
p_returns.append( ret )
p_volatility.append( vol )
p_weights.append( wgt )
rets = np.sum( ret_daily.mean( ) * res[ 'x' ] ) * 250
vol = np.sqrt( res[ 'x' ].T @ covmat @ res[ 'x' ] )
p_volatility = np.array( p_volatility )
p_returns = np.array( p_returns )
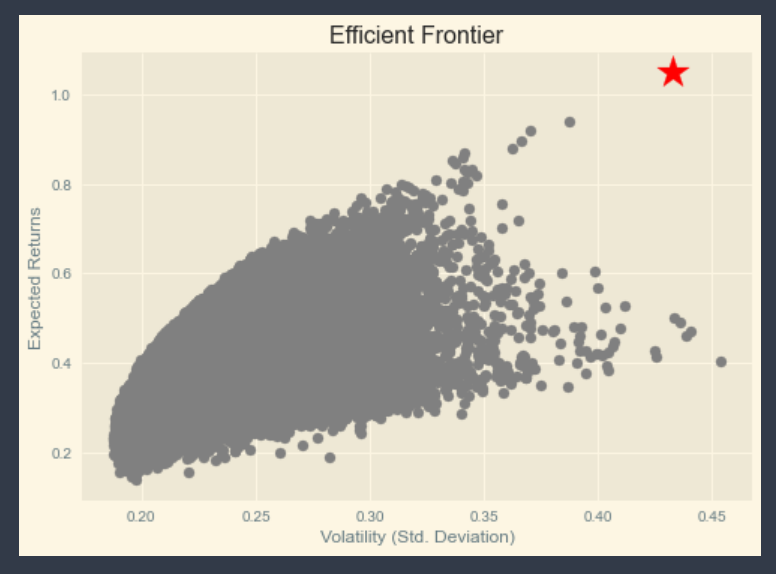
plt.style.use('Solarize_Light2')
plt.scatter( p_volatility, p_returns, c='grey', marker='o', cmap=mpl.cm.jet )
plt.scatter( vol, rets, marker="*", s=500, alpha=1.0, c='red' )
plt.xlabel( 'Volatility (Std. Deviation)' )
plt.ylabel( 'Expected Returns' )
plt.title( 'Efficient Frontier' )
plt.show( )