AI 기초수학 - 벡터와 공간 (2)

[10]

# 랭크

- rank(A) : 선형 독립인 행 혹은 열의 개수

- 랭크의 성질 : 열 랭크과 행 랭크가 같음

 

$$rank(A) = rank(A^T)$$

 

- 선형 독립 (rank = 2)

$$\begin{bmatrix}y1 \\y2 \end{bmatrix} =  \begin{bmatrix}2x_1+7x_2 \\5x_1+1x_2 \end{bmatrix} =  \begin{bmatrix}2 & 5 \\7 & 1 \end{bmatrix}  \begin{bmatrix}x_1 \\x_2 \end{bmatrix} =x1 \begin{bmatrix}2 \\7 \end{bmatrix} +x_2 \begin{bmatrix}5 \\1 \end{bmatrix} $$

 

- 선형 종속 (rank = 1)

$$\begin{bmatrix}y1 \\y2 \end{bmatrix} =  \begin{bmatrix}2x_1+4x_2 \\3x_1+6x_2 \end{bmatrix} =  \begin{bmatrix}2 & 4 \\3 & 6 \end{bmatrix}  \begin{bmatrix}x_1 \\x_2 \end{bmatrix} =x1 \begin{bmatrix}2 \\4 \end{bmatrix} +x_2 \begin{bmatrix}3 \\6 \end{bmatrix}$$

$$=  2x_1\begin{bmatrix}1 \\2 \end{bmatrix} +3x_2 \begin{bmatrix}1 \\2 \end{bmatrix} =(2x_1+3x_2) \begin{bmatrix}1 \\2 \end{bmatrix} $$

 

# 벡터 공간과 부분 공간 기자(basis)

# matrix_rank() >> rank 계산하기

x1 = np.array([[2,7],[5,1]])
print(x1)
print()
print(np.linalg.matrix_rank(x1))

# rank가 2개 >> 선형독립

[[2 7]
 [5 1]]

2

>> rank가 2개 : 선형 독립

 

x10 = np.array([[1,2],[3,5]])
print(x10)
print()
print(np.linalg.matrix_rank(x10))

[[1 2]
 [3 5]]

2

>> rank가 2 = 선형 독립

 

x2 = np.array([[2,4],[3,6]])
print(x2)
print()
print(np.linalg.matrix_rank(x2))

# rank가 1개 >> 선형종속

[[2 4]
 [3 6]]

1

>> rank가 1 = 선형 종속

 

 

 

 

[11]

# 벡터의 덧셈

1)

# 벡터의 덧셈과 뺄셈

x = [2,3]
y = [3,1]

# zip() 이용 : 2 벡터의 1번째 원소끼리 더하고 2번째 원소끼리 더하기 위함

[i+j for i, j in zip(x,y)]

[5, 4]

 

# zip()

print(zip([1,2,3],[4,5,6],[7,8,9]))
print()
print(list(zip([1,2,3],[4,5,6],[7,8,9])))
# 같은 위치끼리 묶어줌

[(1,4,7),(2,5,8),(3,6,9)]

 

2)

import numpy as np

# x,y 리스트를 numpy의 Array 객체로 변화한 후 변수에 저장
u = np.array(x)
v = np.array(y)

#u, v 변수에 덧셈 연사자 적용
w=u+v
print(w)

[5,4]

 

 

 

# 벡터의 뺄셈

1)

x = [2,3]
y = [3,1]

[i- j for i,j in zip(x,y)]

[-1,2]

 

2)

x = [2,3]
y = [3,1]

u = np.array(x)
v = np.array(y)

u-v

array([-1,2])

 

 

 

[13]

# 벡터의 곱셈

1)

# 벡터의 내적(****)

# 벡터의 곱셈
x = [3,4]
c = 8

[c*i for i in x]

[24, 32]

 

>> x 변수에 원소 두 개를 갖는 리스트

     c 변수에 스칼라 상수 8을 저장

 

>> x 리스트 원소 각각에 c 상수를 곱한 결과를 리스트로 변환

 

2)

u = np.array([3,4])
c = 8

u*c

[24, 32]

 

 

 

# 벡터의 내적

- 인공지능 알고리즘에서 유사도 기준은 벡터 간 거리를 이용하는데, 이때 내적 사용

# 벡터의 내적
u = np.array([6,6])
v = np.array([12,6])

np.dot(u,v)
# 벡터의 내적 >> scala
# 72+36 = 108

108

 

>> numpy.dot()

 

 

$$\vec{A}  ·    \vec{B}  =  |  \vec{A}  | |  \vec{B}  | cos \theta $$

 

- 내적 결과는 스칼라(실수)

 

$$\vec{a}  ·    \vec{b}  =  |  \vec{a}  | |  \vec{b}  | cos  0^{0} $$

 

 

 

 

# 벡터의 외적

- 외적 결과가 행렬인 경우 외적

- 3차원 벡터의 외적 결과가 3차원인 경우 벡터곱

 

$$\vec{A}    \times     \vec{B}  =  |  \vec{A}  | |  \vec{B}  | sin   \theta  $$

 

 

1)

# 벡터의 외적

a = (1,3,4)
b = (2,4,6)

def cross(a,b):
    c = [a[1]*b[2]-a[2]*b[1],
         a[2]*b[0]-a[0]*b[2],
         a[2]*b[1]-a[1]*b[2]
         ]
    return c
    
cross(a,b)

[2,2,-2]

 

 

2)

np.cross(a,b)

[2,2,-2]

 

 

 

 

[14]

# 직교 벡터(Orthogonal vector)

- SVM 원리 : 마진을 최대로 하는 결정 경계

 

$$\vec{w}    ·      \vec{u}   \geq   k$$

 

이면, ● 범주, 그렇지 않다면 ■

 

- 내적 한다는 의미는 u를 w에 투영하여 그 길이가 길어서 결정 경계를 넘으면 오른쪽, 짧으면 왼쪽

- 투영 : 물체의 형상을 3차원 공간이나 2차원 평면에 똑같이 옮기는 작업

 

 

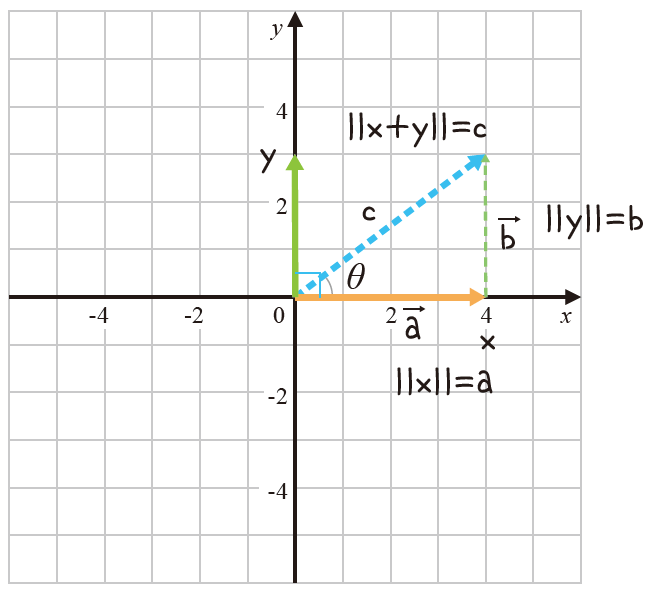
$$ \|  a  \|^2 +\|  b  \|^2 =  \| a+b \|^2$$

 

$$x^Tx+y^Ty=(x+y)^T(x+y)$$

 

- 두 벡터가 직교일 경우, 두 벡터의 내적은 0

 

$$ab =  \begin{bmatrix}a_1,a_2,...,a_n \end{bmatrix}  \begin{bmatrix}b_1\\b_2\\ \vdots \\b_n \end{bmatrix} =  \begin{bmatrix}a_1b_1 , a_2b_2,...,a_nb_n \end{bmatrix} =0$$

 

 

 

# 벡터의 크기 = 벡터의 길이 = 벡터의 norm = |v| = ||v||

 

$$| \vec{a} + \vec{b}| =  \sqrt{(a_1+a_2)^2+(b_2+b_2)^2}  $$

 

- np.linalg.norm()

  ord = 1 : L1 >> 컴퓨터 비전에서 주로 씀

  x = [1,2,3]일 때, ||x|| = 1+2+3  >> 변수 선택 가능

 

  ord = 2 : L2  >> K-평균 클러스터링, K-최근접

  x = [1,2,3]일 때, ||x|| = sqrt(1+2+3)  >> 회귀 분석

 

import numpy as np

a = np.array([1,2])

np.linalg.norm(a)

2.23606797749979

 

# L1 norm

np.linalg.norm(a, ord =1)
# 1+2

3.0

 

# L2 norm

np.linalg.norm(a, ord =2) 
# sqrt(1+2)

2.23606797749979

 

 

 

# 벡터의 거리/유사도

 

- 벡터의 거리 : 두 벡터 간 거리

- 거리가 가까울수록 그 특성(feature)들이 비슷 

 

- 유클리드 거리

  두 벡터 간 직선 거리

 

$$d(x,y) =   \sqrt{(x_1+y_1)^2+(x_2+y_2)^2} $$

 

# 유클리디언 거리
from scipy.spatial import distance

# 두 점 p1, p2 명시

p1 = (1,2,3)
p2 = (4,5,6)

# 두 점 p1, p2 간 유클리드 거리 구하기

distance.euclidean(p1,p2)

# 두 벡터 간 직선 거리

 

 

- 맨해튼 거리

  사각형 격자로 된 지도에서 출발점부터 도착점까지 가로지르지 않고 갈 수 있는 최단 거리를 구하는 공식

$$d(x,y) =  |x_1-x_2| + |y_1-y_2|$$

 

 

# 맨하탄 거리

from math import *

# 두 점 p1, p2 명시

p1 = (1,2,3)
p2 = (4,5,6)

def 맨하탄거리(x,y):
    return sum(abs(a-b) for a, b in zip(x,y))

# d = |x1-x2| + |y1-y2|

맨하탄거리(p1,p2)

# 사각형 격자로 된 지도에서 건물을 피해 목적지를 찾음

>> abs(a-b) : 절댓값 |a-b|

     zip(x,y) : 벡터. x 모든 원소가 y랑 짝을 이룸

 

 

- 코사인 유사도

  두 벡터의 방향이 같을수록 벡터가 비슷하다고 간주하여 두 벡터 간의 각인 코사인 값

 

  각도가 0일 때 가장 크므로 두 벡터가 같은 방향 >> 코사인 유사도 = 최댓값 1

  각도가 90도 가까워 지면 코사인 유사도가 0에 가까워짐

 

$$유사도 = cos \theta  =  \frac{A·B}{||A|| ||B||} $$

 

 

# 코사인 유사도

from numpy import dot
import numpy as np
from numpy.linalg import norm

def cos_sim(a,b):
    return dot(a,b) / (norm(a)*norm(b))

# cos@ = (A dot B) / ||A||*||B||

doc1 = np.array([1,1,1,1,0])
doc2 = np.array([1,0,1,0,1])
doc3 = np.array([2,1,1,1,1])

# 유사도 구하기

print(cos_sim(doc1,doc2)) # 문서1, 문서2 간 코사인 유사도
print(cos_sim(doc1,doc3)) # 문서1, 문서3 간 코사인 유사도
print(cos_sim(doc2,doc3)) # 문서2, 문서3 간 코사인 유사도

# 결론 : 문서1, 문서3 간 코사인 유사도가 가장 높음

0.5773502691896258
0.8838834764831843
0.8164965809277259

>> 문서 1과 3의 유사도가 가장 높음

 

 

 

 

[15]

# 행렬-벡터의 곱

$$A \vec{x}=b $$

 

- 행렬 A가 mxn, 벡터 x가 nx1일 때, 그 결과는 mx1

 

$$ \begin{bmatrix}a_{11} & a_{21} \\a_{12} & a_{22} \end{bmatrix}  \begin{bmatrix}x_1 \\ x_2 \end{bmatrix} = x_1 \begin{bmatrix}a_{11}\\a_{21} \end{bmatrix}+x_2\begin{bmatrix}a_{12}\\a_{22} \end{bmatrix}$$

 

 

# 행렬의 열 공간

- col(A) = span{A의 선형 독립}

- A: span{col(A)}

 

$$A \vec{x} =  \begin{bmatrix}-2 & 4 & 2 \\6 & -3 &3\\5 & -3 & 2\end{bmatrix} \begin{bmatrix}x_1 \\x_2\\x_3 \end{bmatrix}   = \begin{bmatrix}b_1 \\b_2 \\b_3 \end{bmatrix} $$

 

$$x_1 \begin{bmatrix}-2\\6\\5 \end{bmatrix} +x_2 \begin{bmatrix}4\\3\\3 \end{bmatrix} +x_3 \begin{bmatrix}2\\3\\2 \end{bmatrix} = \begin{bmatrix}b_1 \\b_2 \\b_3 \end{bmatrix} $$

 

>> 해를 가지는 경우

- b 벡터가 모두 0인 경우 b= [0,0,0]

 

- x = [1 0 0], [0 1 0], [0 0 1]

 

 

 

# 행렬의 영 공간

$$A \vec{x} = 0$$

 

$$A \vec{x} =  \begin{bmatrix}-2 & 4 & 2 \\6 & -3 &3\\5 & -3 & 2\end{bmatrix} \begin{bmatrix}x_1 \\x_2\\x_3 \end{bmatrix}   = \begin{bmatrix}0 \\0 \\0 \end{bmatrix} $$

 

 

 

# 상삼각행렬

 

$$A =  \begin{bmatrix}1 & 2 & 3 & 1 \\0 & 1 & 1 & 0 \\0 & 0 & 1 & 2\end{bmatrix} $$